KATA PENGANTAR
Puji syukur saya panjatkan kepada Tuhan Yang Maha Esa, yang telah memberikan segala rahmat dan karunia-Nya sehingga Makalah ini berhasil diselesaikan, dengan judul “HIMPUNAN”.
Saya berharap tulisan ini bermanfaat bagi setiap yang membaca dan bisa menambah informasi mengenai himpunan .
Saya menyadari bahwa makalah ini masih jauh dari sempurna, oleh karna itu Saya mengharapkan saran dan kritik yang bersifat membangun untuk lebih menyempurnakan makalah ini. Akhir kata saya ucapkan semoga makalah ini dapat bermanfaat.
Medan, 16 Mei 2012
Iswahyuni
DAFTAR ISI
Kata Pengantar……………………………………..…………………………….…….1
Daftar Isi…………………………………..……………………………………………...2
Bab I PENDAHULUAN……………………....…………….....……………………..3
1.1 Pengertian Himpunan………………..…………………………..4
1.2 Notasi Himpunan………………..….……………………………….5
1.3 Simbol Himpunan……..………..……………………………….…6
BAB II PEMBAHASAN……………………………..………………………….……...7
2.1. Macam – Macam Himpunan…..……………….……………..7
2.1.1. Himpunan Kosong………………….....…...………………..7
2.1.2. Himpunan Semesta……………....………….…….………..7
2.1.3. Himpunan Terbilang………….……………….…………...8
2.1.4. Himpunan Tak Terbilang….......................................8
2.1.5. Himpunan Terbatas………………………………….……..9
2.1.6. Himpunan Tak Terbatas…..………………………………9
2.1.7. Himpunan Bagian…………………………………………….10
2.1.8. Himpunan yang Sama……………………………….……..10
2.1.9. Himpunan yang Ekivalen………………………………….10
2.1.10 Himpunan Saling Lepas…………………………………..10
2.2. Relasi Antar Himpunan………………...….……………….…...11
2.2.1. Subhimpunan…………….……………………………..…..…11
2.2.2. Super Himpunan…………………………………..…….…...11
2.2.3. Kesamaan Dua Himpunan…………….…...……………..12
2.2.4. Himpunan Kuasa…………….……….….…………………...12
2.3. Kardinalitas……………………………………………………………...13
2.3.1. Himpunan Denumerabel .............................................13
2.3.2. Himpunan Tak Berhingga…………..………………………13
2.3.3. Himpunan Berhingga…………….…………………………...14
2.3.4. Himpunan Cacah……………………………………...……….14
2.3.5. Himpunan Non Denumerabel……………………………...14
2.4. Operasi Terhadap Himpunan………………………...14
2.4.1. Irisan…………………………………………………………14
2.3.4. Himpunan Cacah……………………………………...……….14
2.3.5. Himpunan Non Denumerabel……………………………...14
2.4. Operasi Terhadap Himpunan………………………...14
2.4.1. Irisan…………………………………………………………14
2.4.2. Gabungan……………………………………………………15
2.4.3. Komplemen…………………………………………………15
2.4.4. Selisih…………………………………………………………15
2.4.5. Beda Setangkup…………………………………………...17
2.5. Fungsi Karakteristik…………………………………………18
2.5.1. Representasi
Biner……………………………..………....18
2.6. Perkalian Kartesius…………………………………………...19
2.7.
Perampatan Operasi Himpunan………………………..21
2.8.
Hukum- Hukum Himpunan……………………………….21
2.9.
Prinsip Dualitas………………………………………………….23
2.9.1. Prinsip Dualitas Pada
Himpunan………………….23
2.9.2. Prinsip Inklusi – Eksklusi…………………………….25
2.10.Partisi…………………………………………………………….…...26
2.11.
Himpunan Ganda……………………………………………...27
2.12.
Operasi Antara Dua Buah Multise……….…………..27
2.13.
Pembuktian Pernyataan Perihal Himpunan….28
2.14.
Tipe Set Dalam Bahasa Pascal………………………...31
DAFTARPUSTAKA.....................................................................32
BAB I
PENDAHULUAN
Teori himpunan, yang baru diciptakan pada akhir abad ke-19, sekarang merupakan bagian yang tersebar dalam pendidikan matematika yang mulai diperkenalkan bahkan sejak tingkat sekolah dasar. Teori ini merupakan bahasa untuk menjelaskan matematika modern. Teori himpunan dapat dianggap sebagai dasar yang membangun hampir semua aspek dari matematika dan merupakan sumber dari mana semua matematika diturunkan.
alam matematika, himpunan adalah segala koleksi benda-benda tertentu yang dianggap sebagai satu kesatuan. Walaupun hal ini merupakan ide yang sederhana, tidak salah jika himpunan merupakan salah satu konsep penting dan mendasar dalam matematika modern, dan karenanya, studi mengenai struktur kemungkinan himpunan dan teori himpunan, sangatlah berguna.
Dalam pelajaran aljabar yang pernah kita kenal operasi hitung seperti penjumlahan perkalian, pengurangan pembagian, operasi itu membentuk bilangan baru dari bilangan yang diketahui. Demikian juga dengan operasi himpunan. Pengertian operasi pada himpunan tidak berbeda dengan operasi pada bilangan.
Operasi pada himpunan adalah cara membentuk himpunan baru dari himpunan-himpunan yang diketahui. Operasinya ada yang berbentuk uner dan ada yang berbentuk biner. Operasi uner, bila himpunan baru tersebut dari satu himpunan yang diketahui dan operasi biner bila himpunan baru diperoleh dari dua himpunan.
1.1 Pengertian Himpunan
Himpunan dapat didefinisikan dengan dua cara, yaitu:
§ Enumerasi, yaitu mendaftarkan semua anggota himpunan. Jika terlampau banyak tetapi mengikuti pola tertentu.
Contoh 1.
- Himpunan empat bilangan asli pertama: A = {1, 2, 3, 4}.
- Himpunan lima bilangan genap positif pertama: B = {4, 6, 8, 10}.
- C = {kucing, a, Amir, 10, paku}
- R = { a, b, {a, b, c}, {a, c} }
- C = {a, {a}, {{a}} }
- K = { {} }
- K = { {} }
- Himpunan 100 buah bilangan asli pertama: {1, 2, ..., 100 }
Biasanya, nama himpunan ditulis menggunakan huruf besar, misalnya S, A, atau B, sementara elemen himpunan ditulis menggunakan huruf kecil (a, c, z). Cara penulisan ini adalah yang umum dipakai, tetapi tidak membatasi bahwa setiap himpunan harus ditulis dengan cara seperti itu. Tabel di bawah ini menunjukkan format penulisan himpunan yang umum dipakai.
Himpunan A dikatakan himpunan kosong bila bilangan kardinal dari himpunan A = 0 atau n(A) = 0. Himpunan kosong dinotasikan dengan f (phi) atau
 . Jadi apabila A =
. Jadi apabila A = , maka A = f atau A =
, maka A = f atau A = dan n(A) = 0.
dan n(A) = 0.
Hubungan di antara 8 buah set dengan menggunakan diagram Venn
Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.
1.3 Simbol Himpunan
Simbol-simbol khusus yang dipakai dalam himpunan adalah:
BAB II
PEMBAHASAN
2.1 Macam-macam Himpunan
2.1.1 Himpunan Kosong
Perhatikan contoh di bawah ini!
Contoh 1, 2 dan 3 merupakan contoh himpunan yang tidak memiliki anggota atau n(B) = n(C) = n(D) = 0. Tetapi contoh 4, himpunan E dan F bukan contoh himpunan kosong, karena E memiliki anggota yaitu “0” dan F juga memiliki anggota yaitu f.
2.1.2 Himpunan Semesta
Himpunan semesta biasanya dilambangkan dengan U (Universum) yang berarti himpunan yang memuat semua anggota yang dibicarakan atau kata lainya himpunan dari objek yang sedang dibicarakan. Biasanya himpunan semesta ditetapkan sebelum kita membicarakan suatu himpunan dengan demikian seluruh himpunan lain dalam pembicaraan tersebut merupakan bagian dari himpunan pembicaraan.
maka yang menjadi himpunan semestanya adalah :
2.1.3 Himpunan Terbilang
Himpunan A dikatakan himpunan terbilang bila anggota himpunan A tersebut dapat ditunjukkan atau dihitung satu persatu.
Contoh :
Himpunan A di atas merupakan contoh himpunan terbilang sebab dapat dihitung satu persatu, sekaligus contoh himpunan terhingga sebab n(A) = 3.
Himpunan B di atas merupakan contoh himpunan terbilang, tetapi juga merupakan contoh himpunan tak hingga sebab n(B) = ~.
2.1.4 Himpunan Tak Terbilang
Himpunan A dikatakan tak terbilang bila anggota himpunan A tersebut tidak dapat dihitung satu persatu.
Contoh :
Himpunan R merupakan contoh himpunan tak terbilang, karena anggotanya tak dapat dihitung satu persatu. Himpunan R juga merupakan himpunan tak berhingga, karena n(R) = ~.
2.1.5 Himpunan Terbatas
Himpunan A dikatakan himpunan terbatas bila himpunan A mempunyai batas di sebelah kiri saja disebut himpunan terbatas kiri. Dan jika himpunan tersebut hanya mempunyai batas sebelah kanan disebut himpunan terbatas kanan. Batas sebelah kiri juga disebut batas bawah sedangkan batas sebelah kanan disebut batas atas.
Contoh :
Khusus untuk himpunan tak terbatas yang semesta pembicaraanya bilangan real penulisan himpunanya dapat menggunakan notasi interval.
Contoh:
Himpunan A dikatakan himpunan tak terbatas bila himpunan tersebut tidak memiliki batas.
Contoh:
2.1.7 Himpunan Bagian
Himpunan A dikatakan himpunan bagian dari himpuan B jika dan hanya jika setiap elemen A merupakan elemen dari B. dalam hal ini B dikatakan superset dari A. notasinya A  B.
B.
Contoh:
Misalkan A = { 1, 2, 3 } dan B = {1, 2, 3, 4, 5}, maka A  B.
B.
2.1.8 Himpunan yang Sama
Himpunan A dikatakan sama dengan himpunan B, jika dan hanya jika setiap elemen A merupakan elemen B dan sebaliknya. Notasinya A = B <—> A  B.
B.
Contoh:
Jika A = { a, b, c } dan B = { c, a, b } maka A = B
2.1.9 Himpunan yang Ekivalen
Himpunan A dikatakan ekivalen dengan himpunan B jika dan hanya jika cardinal dari kedua himpunan tersebut sama. Notasinya A ~ B <—> n(A) = n(B)
Contoh:
Jika A = { 1, 2, 3,4 } dan B = { s, a, p, i } maka A ~ B sebab n(A) = n(B) = 4
2.1.10 Himpunan Saling Lepas
Dua buah himpunan A dan B dikatakan saling lepas jika keduanya tidak memiliki elemen yang sama. Notasi A // B.
Contoh: Jika A = { x|x є P, x < b =" {">
2.2 Relasi antar himpunan
2.2.1 Subhimpunan
Dari suatu himpunan, misalnya A = {apel, jeruk, mangga, pisang}, dapat dibuat himpunan-himpunan lain yang elemen-elemennya adalah diambil dari himpunan tersebut.
- {apel, jeruk}
- {jeruk, pisang}
- {apel, mangga, pisang}
Ketiga himpunan di atas memiliki sifat umum, yaitu setiap anggota himpunan itu adalah juga anggota himpunan A.
Himpunan-himpunan ini disebut sebagai subhimpunan atauhimpunan bagian dari A. Jadi dapat dirumuskan:
B adalah himpunan bagian dari A jika setiap elemen B juga terdapat dalam A.
Kalimat di atas tetap benar untuk B himpunan kosong. Maka  juga subhimpunan dari A. Untuk sembarang himpunan A,
juga subhimpunan dari A. Untuk sembarang himpunan A,
 juga subhimpunan dari A. Untuk sembarang himpunan A,
juga subhimpunan dari A. Untuk sembarang himpunan A,
Definisi di atas juga mencakup kemungkinan bahwa himpunan bagian dari A adalah A sendiri.Untuk sembarang himpunan A,
Istilah subhimpunan dari A biasanya berarti mencakup A sebagai subhimpunannya sendiri. Kadang-kadang istilah ini juga dipakai untuk menyebut himpunan bagian dari A, tetapi bukanA sendiri. Pengertian mana yang digunakan biasanya jelas dari konteksnya.
Subhimpunan sejati dari A menunjuk pada subhimpunan dari A, tetapi tidak mencakup A sendiri.
Kebalikan dari subhimpunan adalah superhimpunan, yaitu himpunan
yang lebih besar yang mencakup himpunan tersebut.
Himpunan A dan B disebut sama, jika setiap anggota A adalah anggota B, dan sebaliknya, setiap
anggota B adalah anggota A.
Atau Definisi di atas sangat berguna untuk membuktikan
bahwa dua himpunan A dan B adalah sama. Pertama, buktikan dahulu A adalah subhimpunan B, kemudian buktikan bahwa B adalah subhimpunan A.
2.2.3.
Kesamaan dua himpunan
Himpunan A dan B disebut sama, jika setiap anggota A adalah anggota B, dan sebaliknya, setiap
anggota B adalah anggota A.
Atau Definisi di atas sangat berguna untuk membuktikan
bahwa dua himpunan A dan B adalah sama. Pertama, buktikan dahulu A adalah subhimpunan B, kemudian buktikan bahwa B adalah subhimpunan A.
2.2.4.
Himpunan Kuasa
Himpunan kuasa atau himpunan pangkat (power set) dari A adalah himpunan yang terdiri dari
seluruh himpunan bagian dari A.
Notasinya adalah

{ { },
{apel}, {jeruk}, {mangga},
{pisang},
{apel, jeruk}, {apel,
mangga}, {apel, pisang},
{jeruk, mangga}, {jeruk,
pisang}, {mangga, pisang},
{apel, jeruk, mangga}, {apel,
jeruk, pisang}, {apel, mangga, pisang}, {jeruk, mangga, pisang},
{apel, jeruk, mangga, pisang}
}
Banyaknya anggota yang terkandung dalam himpunan kuasa dari A adalah 2 pangkat banyaknya anggota A.
2.3. Kardinalitas
Kardinalitas
dari sebuah himpunan dapat dimengerti sebagai ukuran banyaknya elemen yang
dikandung oleh himpunan tersebut.
Banyaknya
elemen himpunan  adalah
4. Himpunan
adalah
4. Himpunan  juga
memiliki elemen sejumlah 4. Berarti kedua himpunan tersebut ekivalen satu sama
lain, atau dikatakan memiliki kardinalitas yang sama.
juga
memiliki elemen sejumlah 4. Berarti kedua himpunan tersebut ekivalen satu sama
lain, atau dikatakan memiliki kardinalitas yang sama.
Dua
buah himpunan A dan B memiliki
kardinalitas yang sama, jika terdapat fungsi korespondensi satu-satu yang
memetakan A pada B.
Karena dengan mudah kita membuat fungsi  yang
memetakan satu-satu dan kepada himpunan A ke B,
maka kedua himpunan tersebut memiliki kardinalitas yang sama.
yang
memetakan satu-satu dan kepada himpunan A ke B,
maka kedua himpunan tersebut memiliki kardinalitas yang sama.
2.3.1
Himpunan Denumerabel
Jika sebuah himpunan ekivalen dengan himpunan  , yaitu himpunan
bilangan asli, maka himpunan tersebut disebut denumerabel.
Kardinalitas dari himpunan tersebut disebut sebagai
kardinalitas
, yaitu himpunan
bilangan asli, maka himpunan tersebut disebut denumerabel.
Kardinalitas dari himpunan tersebut disebut sebagai
kardinalitas  .
.
 , yaitu himpunan
bilangan asli, maka himpunan tersebut disebut denumerabel.
Kardinalitas dari himpunan tersebut disebut sebagai
kardinalitas
, yaitu himpunan
bilangan asli, maka himpunan tersebut disebut denumerabel.
Kardinalitas dari himpunan tersebut disebut sebagai
kardinalitas  .
.
Himpunan
semua bilangan genap positif merupakan himpunan denumerabel, karena memiliki
korespondensi satu-satu antara himpunan tersebut dengan himpunan bilangan asli,
yang dinyatakan oleh  .
.
 .
.
2.3.2
Himpunan Tak Berhingga
Himpunan A disebut himpunan tak
berhingga apabila tidak memenuhi syarat himpunan berhingga. Himpunan A apabila
anggota-anggotanya sedang dihitung, maka proses perhitunganya tidak akan
berakhir. Dengan perkataan lain himpunan A, n banyak anggotanya tidak dapat
ditentukan/ditulis dengan bilangan cacah.
Contoh
7:
Q=
Apabila kita menghitung anggota himpunan Q, maka proses perhitungan
anggota Q tidak akan berakhir. Jadi Q adalah himpunan tak berhingga dan n(Q) =
~. 2.3.3. Himpunan
Berhingga
Jika sebuah himpunan memiliki kardinalitas yang kurang dari
kardinalitas  , maka himpunan
tersebut adalah himpunan berhingga.
, maka himpunan
tersebut adalah himpunan berhingga.
2.3.4. Himpunan Tercacah
Himpunan disebut tercacah jika himpunan tersebut adalah
berhingga atau denumerabel
2.3.5. Himpunan Non-Denumerabel
Himpunan yang tidak
tercacah disebut himpunan non-denumerabel. Contoh dari himpunan ini adalah
himpunan semua bilangan riil. Kardinalitas dari himpunan jenis ini disebut
sebagai kardinalitas  . Pembuktian
bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian
diagonal.
. Pembuktian
bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian
diagonal.
 . Pembuktian
bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian
diagonal.
. Pembuktian
bahwa bilangan riil tidak denumerabel dapat menggunakan pembuktian
diagonal.
Himpunan bilangan
riil dalam interval (0,1) juga memiliki kardinalitas  karena
terdapat korespondensi satu-satu dari himpunan tersebut dengan himpunan seluruh
bilangan riil, yang salah satunya adalah:
karena
terdapat korespondensi satu-satu dari himpunan tersebut dengan himpunan seluruh
bilangan riil, yang salah satunya adalah:
 karena
terdapat korespondensi satu-satu dari himpunan tersebut dengan himpunan seluruh
bilangan riil, yang salah satunya adalah:
karena
terdapat korespondensi satu-satu dari himpunan tersebut dengan himpunan seluruh
bilangan riil, yang salah satunya adalah:
2.4 Operasi Terhadap Himpunan
2.4.1. Irisan (intersection)
Notasi
: A Ç B = { x |
x Î A dan x Î
B }
Contoh :
Jika A
= {2, 4, 6, 8, 10} dan B = {4, 10,
14, 18},
maka A
Ç
B = {4, 10}
(ii)
Jika A = { 3, 5, 9 } dan B = { -2, 6 }, maka A B = .
Artinya:
A // B
2.4.2.
Gabungan (union)
Notasi
: A È B = { x |
x Î A atau x Î
B }
Contoh.
(i) Jika A
= { 2, 5, 8 } dan B = { 7, 5, 22 },
maka A B = { 2, 5, 7, 8, 22 }
(ii) A = A
2.4.3. Komplemen (complement)
Contoh.
Misalkan
U = { 1, 2, 3, ..., 9 },
Contoh.
A = himpunan
semua mobil buatan dalam negeri
B = himpunan
semua mobil impor
C = himpunan
semua mobil yang dibuat sebelum tahun 1990
D = himpunan
semua mobil yang nilai jualnya kurang dari Rp 100 juta
E = himpunan
semua mobil milik mahasiswa universitas tertentu
“mobil
mahasiswa di universitas ini produksi dalam negeri atau diimpor dari luar
negeri” à
(E Ç A) È (E Ç B) atau E Ç
(A È B)
“semua
mobil produksi dalam negeri yang dibuat sebelum tahun 1990 yang nilai jualnya
kurang dari Rp 100 juta” à A
Ç
C Ç D
“semua mobil impor
buatan setelah tahun 1990 mempunyai nilai jual lebih dari Rp 100 juta” à
2.4.4. Selisih (difference)
Contoh.
(i) Jika A
= { 1, 2, 3, ..., 10 } dan B = { 2,
4, 6, 8, 10 }, maka A – B = { 1, 3, 5, 7, 9 } dan B – A
=
(ii) {1, 3, 5} – {1, 2, 3} = {5}, tetapi {1, 2, 3}
– {1, 3, 5} = {2}
2.4.5. Beda Setangkup (Symmetric Difference)
2.4.5. Beda Setangkup (Symmetric Difference)
Notasi:
A Å B = (A
È
B) – (A Ç
B) = (A – B) È
(B – A)
Contoh 1.
Jika
A = { 2, 4, 6 } dan B = { 2, 3, 5 }, maka A B = { 3, 4, 5, 6 }
Contoh 2.
Misalkan
U = himpunan mahasiswa
P = himpunan
mahasiswa yang nilai ujian UTS di atas 80
Q = himpunan
mahasiswa yang nilain ujian UAS di atas 80
Seorang
mahasiswa mendapat nilai A jika nilai UTS dan nilai UAS keduanya di atas 80,
mendapat nilai B jika salah satu ujian di atas 80, dan mendapat nilai C jika
kedua ujian di bawah 80.
“Semua mahasiswa yang mendapat nilai A” : P Ç Q
“Semua mahasiswa yang mendapat nilai B” : P Å Q
“Ssemua
mahasiswa yang mendapat nilai C” : U
– (P È Q)
(a)
A Å B = B Å A (hukum komutatif)
(b)
(A Å B ) Å C = A Å (B
Å C
) (hukum asosiatif)
TEOREMA 2. Beda setangkup memenuhi sifat-sifat berikut:
2.5.1 Representasi Biner
C ´ D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }
A ´ B = himpunan semua titik di bidang datar

2.5.1 Representasi Biner
C ´ D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }
A ´ B = himpunan semua titik di bidang datar
1. Hukum identitas:
A È Æ = A
A Ç U = A
|
2. Hukum null/dominasi:
A Ç Æ = Æ
A È U = U
|
3. Hukum komplemen:
|
4. Hukum idempoten:
A È A = A
A Ç A = A
|
5. Hukum involusi:
|
6. Hukum penyerapan (absorpsi):
A È(A Ç B) = A
AÇ (AÈB) = A
|
7. Hukum komutatif:
A È B = B È A
A Ç B = B ÇA
|
8. Hukum asosiatif:
AÈ(B ÈC) = (A ÈB) ÈC
AÇ(BÇC) = (AÇB) vC
|
9. Hukum distributif:
A È(B ÇC) = (AÈB)Ç(A ÈC)
A Ç(BÈC) = (A ÇB) È (AÇC)
|
10. Hukum De Morgan:
|
Hukum 0/1
|
1. Hukum identitas:
AÈÆ= A
|
Dualnya:
AÇU = A
|
2. Hukum null/dominasi:
AÇÆ=Æ
|
Dualnya:
AÈU = U
|
3. Hukum komplemen:
|
Dualnya:
|
4. Hukum idempoten:
AÈA = A
|
Dualnya:
AÇ A = A
|
5. Hukum penyerapan:
AÈ(A ÇB) = A
|
Dualnya:
A Ç(A ÈB) = A
|
6. Hukum komutatif:
A ÈB = B ÈA
|
Dualnya:
A ÇB = BÇA
|
7. Hukum asosiatif:
A È(BÈC) = (AÈB)ÈC
|
Dualnya:
AÇ(BÇC) = (AÇB)Ç C
|
8. Hukum distributif:
AÈ(BÇC)=(A ÈB)Ç(AÈC)
|
Dualnya:
AÇ(BÈC) = (AÇB) È(AÇC)
|
9. Hukum De Morgan:
|
Dualnya:
|
10. Hukum 0/1
|
Dualnya:
|

A
|
B
|
C
|
B ÈC
|
A Ç (B È C)
|
A ÇB
|
A ÇC
|
(A Ç B) È (A Ç C)
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
- Himpunan bilangan bulat ditulis sebagai {…, -2, -1, 0, 1, 2, …}.
Keanggotaan
x Î A : x merupakan anggota himpunan A;
x Ï A : x bukan merupakan anggota himpunan A.
§ Pembangun himpunan, tidak dengan mendaftar, tetapi dengan mendeskripsikan sifat-sifat yang harus dipenuhi oleh setiap elemen himpuan tersebut.
Himpunan A tidak mungkin ada, karena jika A ada, berarti harus mengandung anggota yang bukan merupakan anggotanya. Namun jika bukan anggotanya, lalu bagaimana mungkin A bisa mengandung anggota tersebut.
Jadi, Himpunan (set) adalah kumpulan objek-objek yang berbeda. Objek di dalam himpunan disebut elemen, unsur, atau anggota.
2.5. Fungsi Karakteristik
Fungsi
karakteristik menunjukkan apakah sebuah elemen terdapat dalam sebuah himpunan
atau tidak.
Jika konteks
pembicaraan adalah pada sebuah himpunan semesta S, maka setiap himpunan
bagian dari S bisa dituliskan dalam barisan angka 0 dan 1, atau disebut
juga bentuk biner. Bilangan
biner menggunakan angka 1 dan 0 pada setiap digitnya.
Setiap posisi bit dikaitkan dengan masing-masing elemen S, sehingga
nilai 1 menunjukkan bahwa elemen tersebut ada, dan nilai 0 menunjukkan bahwa
elemen tersebut tidak ada. Dengan kata lain, masing-masing bit merupakan fungsi
karakteristik dari himpunan tersebut. Sebagai contoh, jika himpunan S =
{a, b, c, d, e, f, g}, A = {a, c, e, f}, dan B = {b, c,
d, f}, maka:
Himpunan
Representasi Biner
---------------------------- -------------------
a
b c d e f g
S = { a, b, c, d, e, f, g } -->
1 1 1 1 1 1 1
A = { a, c,
e, f } -->
1 0 1 0 1 1 0
B = { b, c, d,
f } -->
0 1 1 1 0 1 0
Cara
menyatakan himpunan seperti ini sangat menguntungkan untuk melakukan
operasi-operasi himpunan, seperti union, interseksi, dan komplemen, karena kita tinggal menggunakan operasi
bit untuk melakukannya.
Representasi
himpunan dalam bentuk biner dipakai oleh kompiler-kompiler Pascal
dan juga Delphi.
2.6.
Perkalian Kartesian (cartesian product)
Notasi:
A ´ B = {(a, b) ½
a Î A dan b Î
B }
Contoh 2.6.1.
(i) Misalkan C
= { 1, 2, 3 }, dan D = { a, b }, maka
(ii) Misalkan A
= B = himpunan semua bilangan riil,
maka
Catatan:
Jika
A dan B merupakan himpunan berhingga, maka: ½A ´
B½ = ½A½ . ½B½.
Pasangan
berurutan (a, b) berbeda dengan (b, a), dengan kata lain (a, b)
¹
(b, a).
Perkalian
kartesian tidak komutatif, yaitu A ´
B ¹ B ´ A
dengan syarat A atau B tidak kosong.
Pada
Contoh 20(i) di atas, D ´
C = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) } ¹ C ´ D.
3.
Jika A
= Æ
atau B = Æ, maka A ´
B = B ´
A =
Æ
Contoh 2.6.2.
Misalkan:
A =
himpunan makanan = { s = soto, g = gado-gado, n = nasi goreng, m = mie
rebus }
B =
himpunan minuman = { c = coca-cola, t = teh, d = es dawet }
Berapa
banyak kombinasi makanan dan minuman yang dapat disusun dari kedua himpunan di
atas?
Jawab:
½A ´
B½ = ½A½×½B½
= 4 ×
3 = 12 kombinasi dan minuman, yaitu {(s,
c), (s, t), (s, d),
(g, c), (g, t), (g,
d), (n, c), (n, t),
(n, d), (m, c), (m,
t), (m, d)}.
Contoh
2.6.3.
Daftarkan semua anggota himpunan berikut:
(a)
P(Æ) (b) Æ ´
P(Æ) (c) {Æ}´
P(Æ) (d) P(P({3}))
Penyelesaian:
P(Æ)
= {Æ}
Æ
´
P(Æ)
= Æ (ket: jika A = Æ atau B = Æ maka A ´
B = Æ)
{Æ}´
P(Æ)
= {Æ}´
{Æ}
= {(Æ,Æ))
P(P({3}))
= P({ Æ, {3} }) = {Æ, {Æ},
{{3}}, {Æ,
{3}} }
2.7.
Perampatan
Operasi Himpunan
Contoh.
(i) A Ç(B1ÈB2È ...ÈBn) = (AÇB1)È(A ÇB2)È...È(AÇBn)
(ii)
Misalkan A = {1, 2}, B
= {a, b}, dan C = {a,
b},
maka
A ´
B ´ C = {(1, a, a), (1, a, b), (1, b, a), (1, b, b), (2, a, a), (2, a, b), (2, b, a), (2, b, b) }
2.8.
Hukum-hukum
Himpunan
2.9.
Prinsip
Dualitas
Prinsip
dualitas: dua konsep yang berbeda dapat dipertukarkan namun tetap memberikan
jawaban yang benar.
Contoh:
AS à
kemudi mobil di kiri depan
Inggris (juga Indonesia) à
kemudi mobil di kanan depan
Peraturan:
(a) di Amerika Serikat,
- mobil harus berjalan di bagian kanan
jalan,
pada
jalan yang berlajur banyak, lajur kiri untuk mendahului,
bila
lampu merah menyala, mobil belok kanan boleh langsung
(b)
di Inggris,
mobil
harus berjalan di bagian kiri jalan,
pada
jalur yang berlajur banyak, lajur kanan untuk mendahului,
bila
lampu merah menyala, mobil belok kiri boleh langsung
Prinsip
dualitas:
Konsep
kiri dan kanan dapat dipertukarkan pada kedua negara tersebut sehingga
peraturan yang berlaku di Amerika Serikat menjadi berlaku pula di Inggris.
2.9.1.
(Prinsip Dualitas pada Himpunan).
Misalkan S adalah suatu kesamaan (identity) yang melibatkan himpunan dan operasi-operasi
seperti È,Ç, dan komplemen. Jika S* diperoleh dari S dengan mengganti È® Ç, Ç®È, Æ® U, U ®Æ, sedangkan komplemen dibiarkan seperti semula,
maka kesamaan S* juga benar dan disebut dual dari kesamaan S.
Contoh.
2.9.2.
Prinsip Inklusi-Eksklusi
Untuk
dua himpunan A dan B:
½A È
B½ = ½A½ + ½B½ – ½A Ç
B½
½A
Å
B½ = ½A½ +½B½ – 2½A Ç
B½
Contoh 2.9.2.
Berapa banyaknya bilangan bulat antara 1 dan
100 yang habis dibagi 3 atau 5?
Penyelesaian:
A
= himpunan bilangan bulat yang habis dibagi 3,
B
= himpunan bilangan bulat yang habis dibagi 5,
A Ç
B =
himpunan bilangan bulat yang habis dibagi 3 dan 5 (yaitu himpunan
bilangan bulat yang habis dibagi oleh KPK – Kelipatan Persekutuan Terkecil –
dari 3 dan 5, yaitu 15),
yang
ditanyakan adalah ½A
È
B½.
½A½ = ë100/3û = 33,
½B½ = ë100/5û = 20,
½A Ç
B½ = ë100/15û = 6
½A
È
B½ = ½A½ + ½B½ – ½A
Ç
B½ = 33 + 20 – 6 =
47
Jadi,
ada 47 buah bilangan yang habis dibagi 3 atau 5.
Untuk
tiga buah himpunan A, B, dan C, berlaku
½A È
B È C½ = ½A½ + ½B½ + ½C½ – ½A
Ç
B½ –
½A
Ç
C½ – ½B
Ç
C½ + ½A Ç
B Ç C½
Untuk
himpunan A1, A2, …, Ar, berlaku:
½Ai
Ç
Aj Ç
Ak½
+ … + (-1)r-1 ½A1
Ç
A2 Ç
… Ç
Ar½
2.10.
Partisi
Partisi dari sebuah himpunan A adalah sekumpulan himpunan bagian
tidak kosong A1, A2, … dari A sedemikian sehingga:
A1
È
A2 È
… = A, dan
Ai
Ç
Aj = Æ
untuk i ¹
j
Contoh.
Misalkan
A = {1, 2, 3, 4, 5, 6, 7, 8}, maka {
{1}, {2, 3, 4}, {7, 8}, {5, 6} } adalah partisi A.
2.11.
Himpunan Ganda
Himpunan
yang elemennya boleh berulang (tidak harus berbeda) disebut himpunan ganda (multiset).
Contohnya,
{1, 1, 1, 2, 2, 3}, {2, 2, 2}, {2, 3, 4}, {}.
Multiplisitas
dari suatu elemen pada himpunan ganda adalah jumlah kemunculan elemen tersebut
pada himpunan ganda. Contoh: M = { 0, 1, 1, 1, 0, 0, 0, 1 },
multiplisitas 0 adalah 4.
Himpunan
(set) merupakan contoh khusus dari suatu multiset, yang dalam hal ini multiplisitas dari setiap elemennya
adalah 0 atau 1. Kardinalitas dari suatu
multiset didefinisikan sebagai
kardinalitas himpunan padanannya (ekivalen), dengan mengasumsikan elemen-elemen
di dalam multiset semua berbeda.
2.12.
Operasi Antara Dua Buah Multiset:
Misalkan
P dan Q adalah multiset:
P Q adalah suatu multiset yang multiplisitas elemennya sama dengan multiplisitas
maksimum elemen tersebut pada himpunan P
dan Q.
Contoh
1: P = { a, a, a, c,
d, d } dan Q ={ a, a,
b, c, c },
P Q = { a, a, a, b, c, c, d,
d }
P Q adalah suatu multiset yang multiplisitas elemennya sama dengan multiplisitas
minimum elemen tersebut pada himpunan P
dan Q.
Contoh
2: P = { a, a, a, c,
d, d } dan Q = { a, a,
b, c, c }
P Q = { a, a, c }
3. P – Q
adalah suatu multiset yang
multiplisitas elemennya sama dengan:
multiplisitas elemen tersebut pada P dikurangi multiplisitasnya pada Q, jika selisihnya positif
0, jika selisihnya nol atau negatif.
Contoh 1: P
= { a, a, a, b, b,
c, d, d, e } dan Q = { a, a, b, b,
b, c,
c, d, d, f
} maka P – Q = { a, e }
P + Q, yang didefinisikan sebagai jumlah (sum) dua buah himpunan ganda, adalah
suatu multiset yang multiplisitas
elemennya sama dengan penjumlahan dari multiplisitas elemen tersebut pada P dan Q.
Contoh
2: P = { a, a, b, c,
c } dan Q = { a, b, b,
d },
P
+ Q = { a, a, a, b,
b, b, c, c, d
}
2.13.
Pembuktian
Pernyataan Perihal Himpunan
Pernyataan
himpunan adalah argumen yang menggunakan notasi himpunan.
Pernyataan
dapat berupa:
Kesamaan
(identity)
Contoh 1:
Buktikan
“A Ç (B È C) = (A Ç
B) È (A Ç C)” Implikasi
Contoh 2:
Buktikan
bahwa “Jika A Ç
B = Æ
dan A Í
(B È
C) maka selalu berlaku bahwa A Í C”.
1. Pembuktian dengan menggunakan
diagram Venn
Contoh
26. Misalkan A, B, dan C adalah himpunan.
Buktikan A Ç
(B È C) = (A Ç
B) È (A Ç C) dengan diagram Venn.
Bukti:
A Ç (B È C) (A Ç B) È (A Ç C)
Kedua
digaram Venn memberikan area arsiran yang sama.
Terbukti
bahwa A Ç
(B È C) = (A Ç
B) È (A Ç C).
Diagram
Venn hanya dapat digunakan jika himpunan yang digambarkan tidak banyak
jumlahnya. Metode ini mengilustrasikan ketimbang membuktikan
fakta. Diagram Venn tidak dianggap
sebagai metode yang valid untuk pembuktian secara formal.
2. Pembuktikan dengan menggunakan
tabel keanggotaan
Contoh
27. Misalkan A, B, dan C adalah himpunan.
Buktikan bahwa A Ç
(B È C) = (A Ç
B) È (A Ç C).
Bukti:
Karena
kolom A Ç
(B È C) dan kolom (A Ç
B) È (A Ç C) sama, maka A Ç
(B È C) = (A Ç
B) È (A Ç C).
3. Pembuktian dengan menggunakan
aljabar himpunan.
Bukti:
= A
Ç
U (Hukum komplemen)
= A (Hukum identitas)
Contoh 3 : Misalkan A
dan B himpunan. Buktikan bahwa A È (B – A)
= A È B
Bukti:
= (A
È
B) Ç U (Hukum
komplemen)
= A
È
B (Hukum
identitas)
Contoh 4. Buktikan bahwa untuk sembarang himpunan A dan B, bahwa
Bukti:
= U
Ç (A Ç
B) (H.
komplemen)
= A È B (H.
identitas)
(ii) adalah dual dari (i)
= Æ È (A Ç
B) (H.
komplemen)
= A Ç B (H.
identitas)
4. Pembuktian dengan menggunakan
definisi
Metode
ini digunakan untuk membuktikan pernyataan himpunan yang tidak berbentuk
kesamaan, tetapi pernyataan yang berbentuk implikasi. Biasanya di dalam
implikasi tersebut terdapat notasi himpunan bagian (Í
atau Ì).
Contoh 5: Misalkan A dan B himpunan. Jika
A Ç B = Æ dan A Í (B È C) maka A Í
C. Buktikan!
Bukti:
Dari
definisi himpunan bagian, P Í
Q jika dan hanya jika setiap x Î P juga Î Q. Misalkan x Î
A. Karena A Í
(B È C), maka dari definisi himpunan bagian, x juga Î (B È C).
Dari
definisi operasi gabungan (È), x
Î
(B È C) berarti x Î
B atau x Î
C.
Karena x
Î
A dan A Ç
B = Æ, maka x Ï B
Dari
(i) dan (ii), x Î
C harus benar. Karena "x
Î
A juga berlaku x Î
C, maka dapat disimpulkan A Í
C .
2.14.
Tipe Set
dalam Bahasa Pascal
Bahasa
Pascal menyediakan tipe data khusus untuk himpunan, yang bernama set.
Tipe set menyatakan himpunan kuasa dari tipe ordinal (integer, character).
Contoh 1:
type
HurufBesar = ‘A’..‘Z’; { enumerasi
}
Huruf = set of HurufBesar;
var
HurufKu : Huruf;
Nilai
untuk peubah HurufKu dapat diisi dengan pernyataan berikut:
HurufKu:=[‘A’, ‘C’, ‘D’];
HurufKu:=[‘M’];
HurufKu:=[]; { himpunan kosong }
Operasi
yang dapat dilakukan pada tipe himpunan adalah operasi gabungan, irisan, dan
selisih seperti pada contoh berikut:
{gabungan}
HurufKu:=[‘A’, ‘C’, ‘D’] + [‘C’,
‘D’, ‘E’];
{irisan}
HurufKu:=[‘A’, ‘C’, ‘D’] * [‘C’,
‘D’, ‘E’];
{selisih}
HurufKu:=[‘A’,
‘C’, ‘D’] - [‘C’, ‘D’, ‘E’];
Uji
keanggotaan sebuah elemen di dalam himpunan dilakukan dengan menggunakan
opeator in seperti contoh berikut:
if ‘A’ in HurufKu then ...
Di
dalam kakas pemrograman Delphi, set sering digunakan untuk
mengindikasikan flag. Misalnya
himpunan icon untuk window:
type
TBorderIcon=(biSystemMenu, biMinimize,
biMaximaze);
Huruf = set of TBoderIcon;
DAFTAR PUSTAKA
1. Halmos, Paul R., Naive Set Theory, Princeton, N.J.: Van Nostrand (1960) ISBN 0-387-90092-6
2. Stoll, Robert R., Set Theory and Logic, Mineola, N.Y.: Dover Publications (1979) ISBN 0-486-63829-4
By : Cutt Iswahyuni





















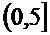















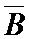






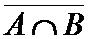 =
=



















copy donghggg
BalasHapusbole kak?
boleh dong?
BalasHapusboleh dong, kenapa ngak :)
BalasHapuskirim pesan ke facebook aja yaa, ntar saya kasih copiannya melalui fb :)
mau dongg kaka
BalasHapuskirim alamat email nya ke facebook kakak ya :'))
BalasHapussalam.., ka saya juga mau donk... :)
BalasHapussaya kirim alamat email saya ke fb kaka ya... :)
terima kasih. mohon bantuannya nya ya ka...
Rizki Darmawan
KOPAS DONG
BalasHapusboleh, kirim alamat email ke pesan fb saya ya (https://www.facebook.com/cutiswahyunii)
BalasHapus