Sebuah Perusahaan akan memproduksi 2 jenis prouduk yaitu lemari dan kursi. untuk memproduksi 2 produk tersebut dibutuhkan 2 kegiatan yaitu proses perakitan dan pengecatan. perusahaan menyediakan waktu 56 jam untuk proses perakitan dan 60 jam untuk proses pengecatan. untuk memproduksi 1 unit lemari diperlukan waktu 8 jam perakitan dan 5 jam pengecatan. utnuk produksi 1 unit kursi diperlukan 7 jam perakitan dan 12 jam pengecatan. jika masing-masing harga produk adalah Rp.200.000 untuk lemari dan Rp.100.000 untuk kursi. tentukan solusi optimal agar mendapatkan untung maksimal ?
a. Fungsi Kendala
x = lemari
y = kursi
y = kursi
| Produk | Waktu Perakitan | Waktu Pengecatan | Harga/unit |
| Lemari (x) | 8 jam | 5 jam | 200 |
| Kursi (y) | 7 jam | 12 jam | 100 |
| Waktu yang tersedia | 56 jam | 60 jam | - |
Fungsi Tujuan
Z = 100x + 200y
Z = 100x + 200y
Fungsi kendala
(i) 8x +7y=56
(ii) 5x+12y=60
(i) 8x +7y=56
(ii) 5x+12y=60
b. Menetukan Koordinat
Persamaan (i)
Jika x=0 jika y=0
8x+7y =56 8x+7y =56
8(0)+7y=56 8x+7(0)=56
7y=56 8x=56
y=56/7 x=56/8
y=8 x=7
Titik Potong : [{0,8} dan {7,0}]
Persamaan (ii)
Jika x=0 jikay=(0)
5x+12y=60 5x+12y=60
5(0)+12y=60 5x+12(0)=60
12y=60 5y=60
y=60/12 y=60/5
y=5 y=12
Titik Potong : [{0,5} dan {12,0}]
5x+12y=60 5x+12y=60
5(0)+12y=60 5x+12(0)=60
12y=60 5y=60
y=60/12 y=60/5
y=5 y=12
Titik Potong : [{0,5} dan {12,0}]
c. Grafik
d. Menyelesaikan permasalahan dengan eliminasi
5x+12y=605x+12(3,3)=60
5x+39,6=60
5x=60 – 39
5x=20,4
x=20,45/5
x=4,08
Titik potong : [{4,08;3,3}]
e. penetuan solusi
untuk koordinat (0,5) untuk koordinat (7,0)
Z = 100x + 200y Z = 100x + 200y
= 100(0) + 200 (5) = 100(7) + 200 (0)
= 0 + 1000 = 700 + 0
= 1000 = 700
untuk (4,08 ; 3,3)
Z = 100x + 200y
= 100(4,08) + 200(3,3)
= 408 + 660
= 1068
Z = 100x + 200y Z = 100x + 200y
= 100(0) + 200 (5) = 100(7) + 200 (0)
= 0 + 1000 = 700 + 0
= 1000 = 700
untuk (4,08 ; 3,3)
Z = 100x + 200y
= 100(4,08) + 200(3,3)
= 408 + 660
= 1068

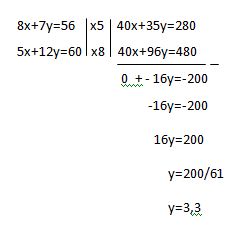
parah yang punya blog ni akh :D
BalasHapuseihhhhhhhhh :/
BalasHapusapa lu bilang jarr :D
KLIK SPONSOR BERIKUT UNTUK MENDAPATKAN PULSA GRATIS
BalasHapus